作者:微信小助手
发布时间:2025-03-05T09:01:16
向量化(Vectorization)是一种将数据或操作转换为向量的过程,以便利用并行计算和高效处理。向量化将非数值数据(如文本、图像)转换为数值向量,以便计算机处理。而向量化在AIGC中非常的常见,例如知识库对话等等。如果大家感兴趣,后面专门来聊聊。 向量长什么样?例如:[0.25, -0.1, 0.7],向量化后的数据通常是一个数值数组 那我们如何将文本向量化呢,有很多种方式,这里我们使用Embedding。 Embedding(嵌入)是一种将高维、离散的数据(如单词、类别、图像等)映射到低维、连续的向量空间的技术。这些向量能够捕捉数据的语义或特征信息,广泛应用于自然语言处理(NLP)、推荐系统和机器学习等领域。 例如通过下面的代码我们可以将文本转换为向量化: 向量数据库是一种专门设计用于存储和查询向量数据的数据库,而ElasticSearch就可以用来存储我们的向量 这里我们定义test2 文档的内容如下(my_vector 和 my_text): 假设 text1 的向量为 [0.5, 10, 6] 那么我们存入了向量是不是也要查询,假如我们有一个字符串 test2 向量化之后的数据为 [-0.5, 10, 7] 这个请求使用了 script_score 查询,结合 cosineSimilarity 函数来计算文档中 my_vector 字段与给定查询向量之间的余弦相似度。为了确保查询结果的分数是非负的,cosineSimilarity 的结果加了 1.0。 余弦相似度(Cosine Similarity) 定义:余弦相似度通过计算两个向量的夹角余弦值来衡量它们的相似性。公式为: 其中,A⋅BA⋅B 是向量的点积,∥A∥∥A∥ 和 ∥B∥∥B∥ 是向量的模。 用途:常用于文本相似度计算、推荐系统等场景,因为它对向量的绝对大小不敏感,只关注方向。 向量维度:确保 queryVector 的维度与索引映射中定义的 my_vector 字段的维度一致,my_vector 的维度是 3,因此 queryVector 也必须是 3 维向量。如果维度不匹配,Elasticsearch 将返回错误。 评分范围:cosineSimilarity 的结果范围是 [-1, 1],其中 1 表示完全相同,-1 表示完全相反。为了确保评分是非负的,通常会将结果加 1.0,这样评分范围变为 [0, 2]。我们可以根据需要调整这个偏移量。 除了余弦相似度这种算法,我们还可以使用 计算点积:dotProduct 来计算 点积(Dot Product) 定义:点积是两个向量对应元素相乘后的和。公式为: 用途:点积可以用于衡量两个向量的相似性,尤其是在向量已经归一化的情况下。它也是许多机器学习算法中的基本操作。 曼哈顿距离(Manhattan Distance, L1 Norm) 定义:曼哈顿距离是两个向量在标准坐标系下的绝对差之和。公式为: 用途:适用于需要衡量向量之间绝对差异的场景,如路径规划、图像处理等。 欧几里得距离(Euclidean Distance, L2 Norm) 定义:欧几里得距离是两个向量之间的直线距离。公式为: 用途:广泛用于聚类分析、图像识别等领域,因为它直观地反映了向量之间的几何距离。 除了上面的内置函数,这些算法在信息检索、推荐系统、聚类分析等领域有广泛应用。我们甚至可以自定义函数: 脚本逻辑 向量化作为一种将高维、离散数据转换为低维、连续向量的技术,已经成为现代数据科学和机器学习领域的核心工具之一。通过将文本、图像、类别等复杂数据转化为数值向量,我们不仅能够更高效地处理和分析这些数据,还能捕捉到数据之间的深层次关系和语义信息。 例如我们公司就是在将文本转存为向量化存储到ES中,从而加入更好的算法,例如RAG Reranker重排,确保能检索到最相关的内容。from transformers import BertTokenizer, BertModel
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
model = BertModel.from_pretrained('bert-base-uncased')
inputs = tokenizer("I love programming", return_tensors="pt")
outputs = model(**inputs)
embeddings = outputs.last_hidden_state # 获取单词或句子的向量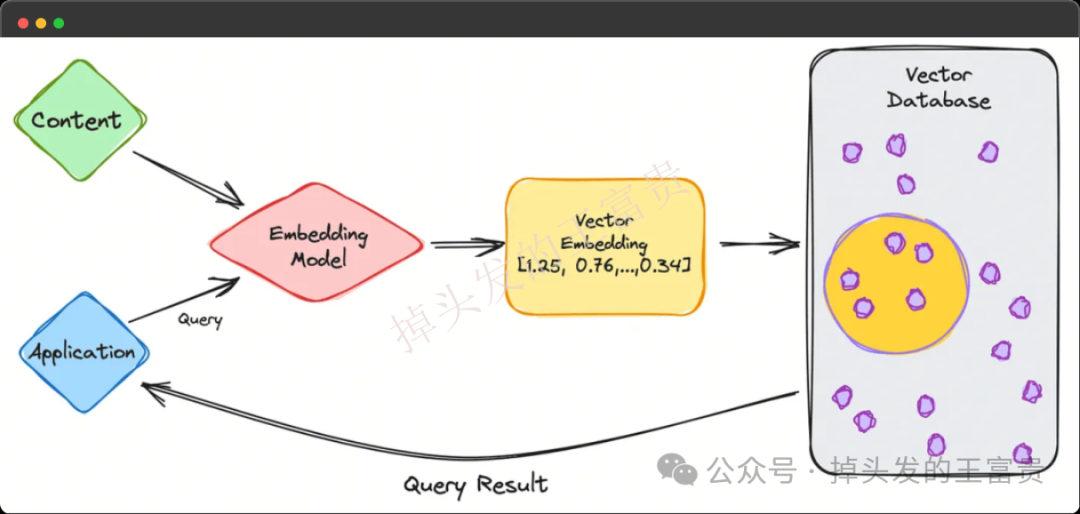
定义向量字段
PUT /test2
{
"mappings": {
"properties": {
"my_vector": {
"type": "dense_vector",
"dims": 3
},
"my_text" : {
"type" : "keyword"
}
}
}
}my_vector 是一个密集向量(dense vector),用于存储多维数据,如嵌入式表示;而 my_text 是一个关键字类型的字段,通常用于精确匹配和聚合。dims: 3:指定向量的维度为 3。这意味着每个文档的 my_vector 字段将包含 3 个浮点数。添加向量
PUT /test2/_doc/2
{
"my_text" : "text1",
"my_vector" : [0.5, 10, 6]
}my_text: "text1":设置 my_text 字段的值为 "text1"。根据之前的映射,my_text 是一个 keyword 类型的字段,适用于精确匹配和聚合。my_vector: [0.5, 10, 6]:设置 my_vector 字段的值为 [0.5, 10, 6],my_vector 是一个 dense_vector 类型的字段,维度为 3。余弦相似度:cosineSimilarity
POST /test2/_search
{
"query": {
"script_score": {
"query": {
"match_all": {}
},
"script": {
"source": "cosineSimilarity(params.queryVector, 'my_vector') + 1.0",
"params": {
"queryVector": [-0.5, 10, 7]
}
}
}
}
}cosineSimilarity 函数:cosineSimilarity 是 Elasticsearch 提供的一个内置函数,用于计算两个向量之间的余弦相似度。它适用于 dense_vector 类型的字段。
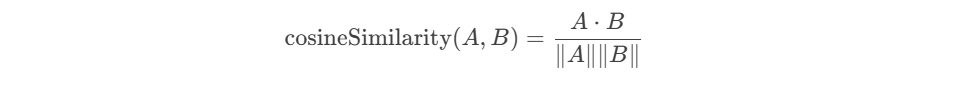
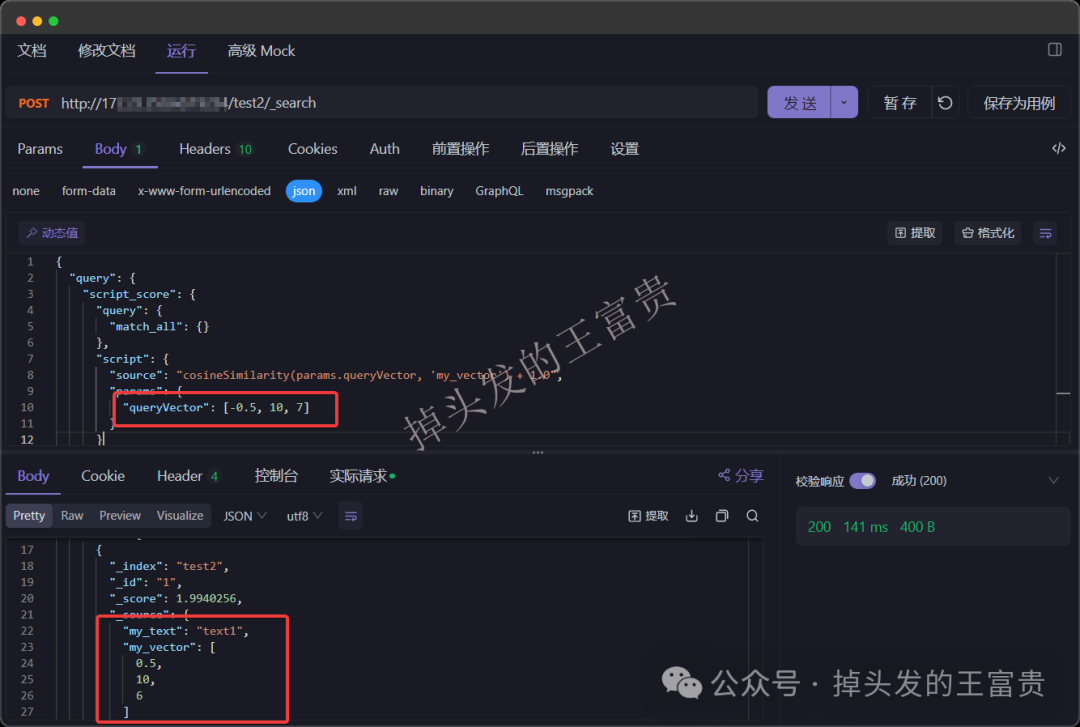
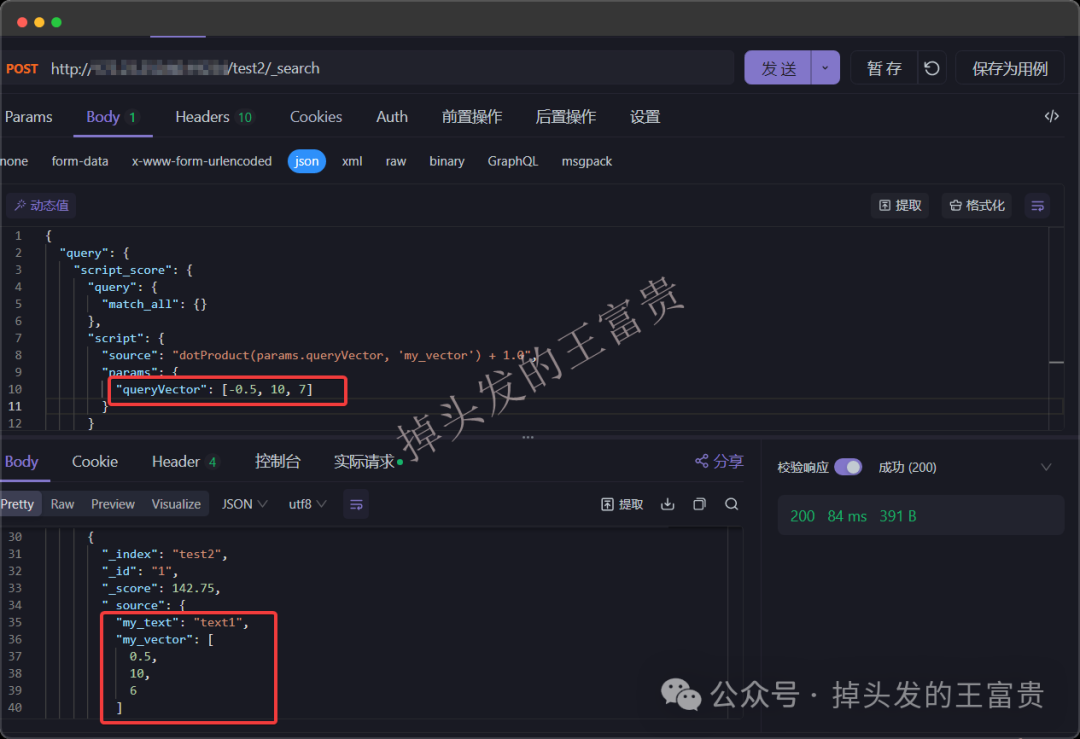
计算点积:dotProduct
POST /test2/_search
{
"query": {
"script_score": {
"query": {
"match_all": {}
},
"script": {
"source": "dotProduct(params.queryVector, 'my_vector') + 1.0",
"params": {
"queryVector": [-0.5, 10, 7]
}
}
}
}
}
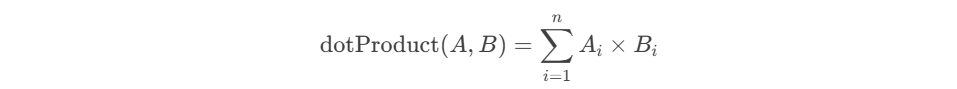
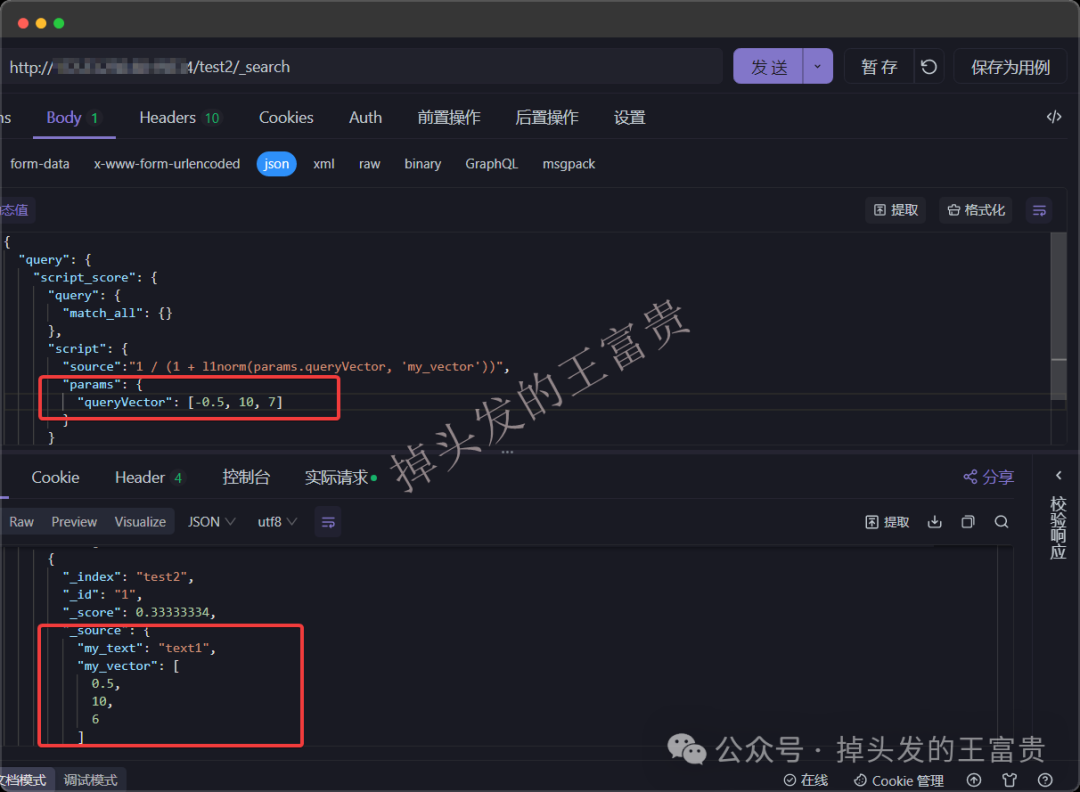
曼哈顿距离:l1norm
POST /test2/_search
{
"query": {
"script_score": {
"query": {
"match_all": {}
},
"script": {
"source":"1 / (1 + l1norm(params.queryVector, 'my_vector'))",
"params": {
"queryVector": [-0.5, 10, 7]
}
}
}
}
}
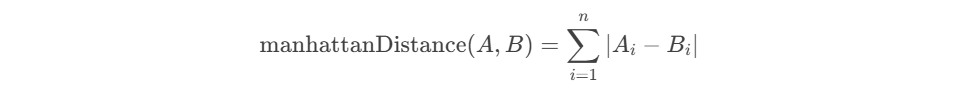
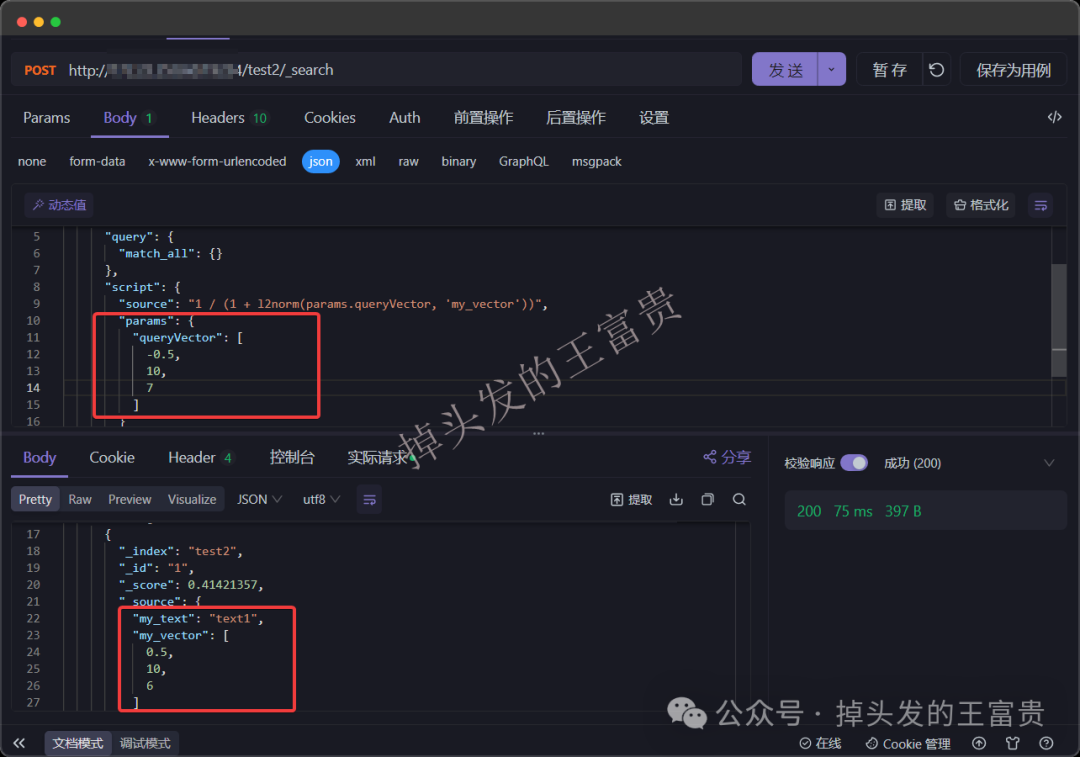
欧几里得距离:l2norm
POST /test2/_search
{
"query": {
"script_score": {
"query": {
"match_all": {}
},
"script": {
"source": "1 / (1 + l2norm(params.queryVector, 'my_vector'))",
"params": {
"queryVector": [
-0.5,
10,
7
]
}
}
}
}
}

自定义函数
POST /test2/_search
{
"query": {
"script_score": {
"query": {
"match_all": {}
},
"script": {
"source": "float[] v = doc['my_vector'].vectorValue; float vm = doc['my_vector'].magnitude; float dotProduct = 0; for (int i = 0; i < v.length; i++) { dotProduct += v[i] * params.queryVector[i]; } return dotProduct / (vm * (float) params.queryVectorMag);",
"params": {
"queryVector": [
-0.5,
10,
7
],
"queryVectorMag": 5.25357
}
}
}
}
}float[] v = doc['my_vector'].vectorValue; // 获取文档中的向量
float vm = doc['my_vector'].magnitude; // 获取文档向量的模
float dotProduct = 0; // 初始化点积
for (int i = 0; i < v.length; i++) { // 遍历向量维度
dotProduct += v[i] * params.queryVector[i]; // 计算点积
}
return dotProduct / (vm * (float) params.queryVectorMag); // 返回余弦相似度
POST /test2/_search:在索引 test2 中执行搜索。
query:定义查询逻辑。
script_score:使用自定义脚本对文档评分。
match_all:匹配所有文档。
script:定义评分脚本。
params:传递给脚本的参数,包括查询向量 queryVector 和它的模 queryVectorMag。
